The advent of social networks poses severe threats
on user privacy as adversaries can de-anonymize users’identities
by mapping them to correlated cross-domain networks. Without
ground-truth mapping, prior literature proposes various cost
functions in hope of measuring the quality of mappings. However,
there is generally a lacking of rationale behind the cost functions,
whose minimizer also remains algorithmically unknown.
We jointly tackle above concerns under a more practical
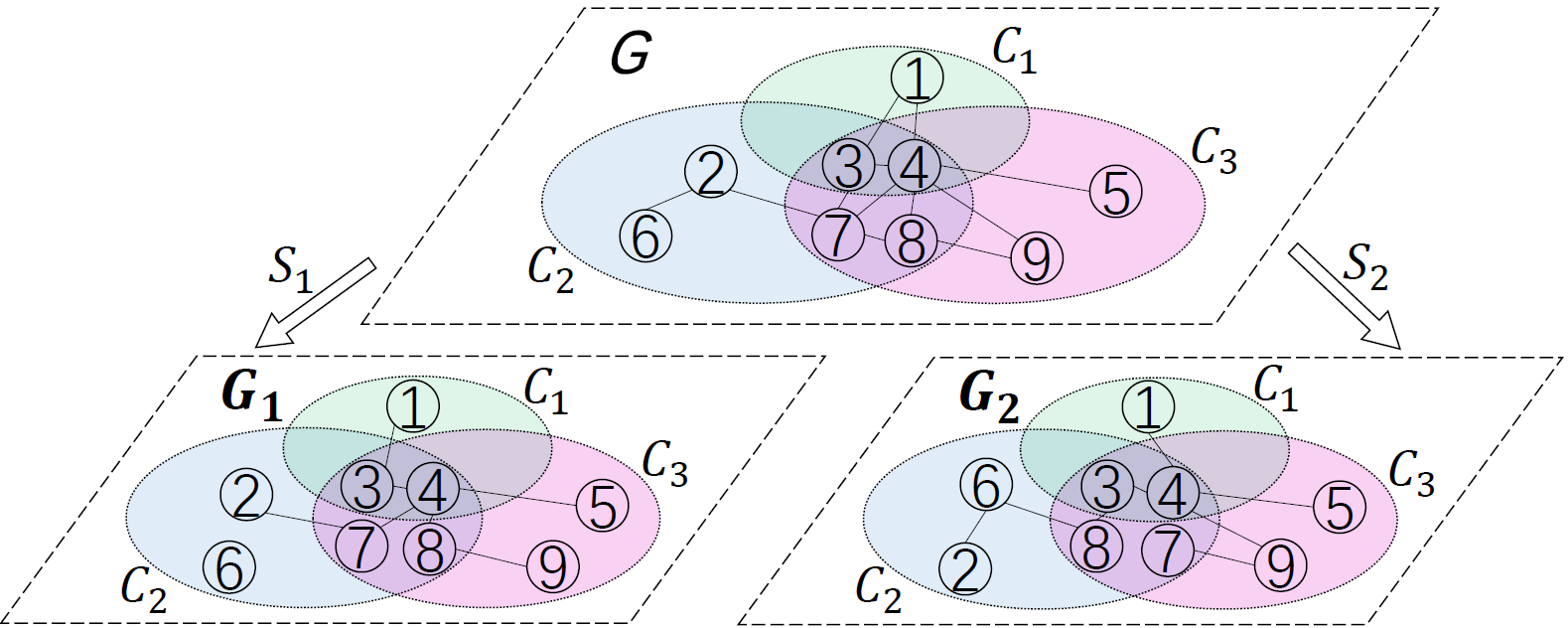
social network model parameterized by overlapping communities,
which, neglected by prior art, can serve as side information
for de-anonymization. Regarding the unavailability of ground-truth mapping to adversaries, by virtue of the Minimum Mean
Square Error (MMSE), our first contribution is a well-justified
cost function minimizing the expected number of mismatched
users over all possible true mappings. While proving the NP-hardness of minimizing MMSE, we validly transform it into the
weighted-edge matching problem (WEMP), which, as disclosed
theoretically, resolves the tension between optimality and complexity: (i) WEMP asymptotically returns a negligible mapping
error in large network size under mild conditions facilitated by
higher overlapping strength; (ii) WEMP can be algorithmically
characterized via the convex-concave based de-anonymization
algorithm (CBDA), perfectly finding the optimum of WEMP.
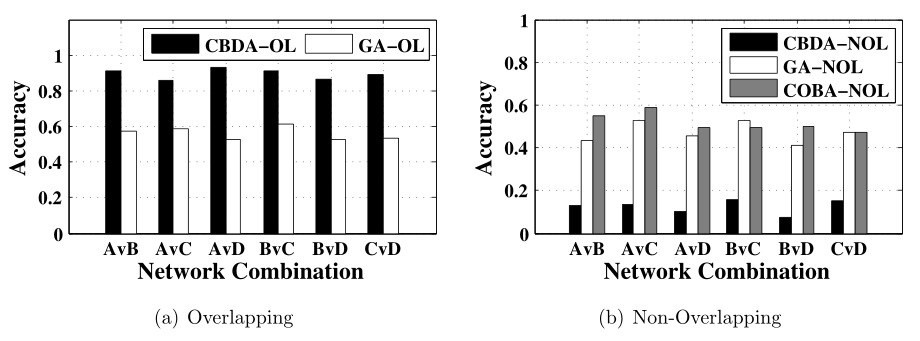
Extensive experiments further confirm the effectiveness of CBDA
under overlapping communities, in terms of averagely 90% re-identified users in the rare true cross-domain co-author networks
when communities overlap densely, and roughly 70% enhanced
re-identification ratio compared to non-overlapping cases.